Question

Find the equation of the line perpendicular to y =
3x + 6 and containing the point (-9,-5).

Answer 1

The equation of the line perpendicular to y = 3x + 6 and containing the point (-9,-5) is
`y = (-1)/(3)x - 8`

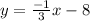
Solution:

Given that line perpendicular to y = 3x + 6 and containing the point (-9, -5)

We have to find the equation of line

The slope intercept form is given as:

y = mx + c ------ eqn 1

Where "m" is the slope of line and "c" is the y - intercept

Let us first find the slope of line

The given equation of line is y = 3x + 6

On comparing the given equation of line y = 3x + 6 with eqn 1, we get,

m = 3

Thus the slope of given equation of line is 3

We know that product of slopes of given line and slope of line perpendicular to given line is equal to -1

Slope of given line
`*` slope of line perpendicular to given line = -1

`3 * \text{ slope of line perpendicular to given line }= -1`

`\text{ slope of line perpendicular to given line } = (-1)/(3)`

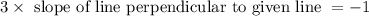
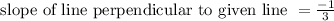
Let us now find the equation of line with slope
`m = (-1)/(3)` and containing the point (-9, -5)

Substitute
`m = (-1)/(3)` and (x, y) = (-9, -5) in eqn 1

`-5 = (-1)/(3)(-9) + c\\\\-5 = 3 + c\\\\c = -8`

Thus the required equation of line is:

Substitute
`m = (-1)/(3)` and c = -8 in eqn 1

`y = (-1)/(3)x - 8`

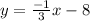
Thus the required equation of line perpendicular to given line is found