Question

Suppose we want a 90% confidence interval for the average amount of time (in minutes) spent per week on homework by the students in a large introductory statistics course at a large university. The interval is to have a margin of error of 3 minutes, and the amount spent has a Normal distribution with a standard deviation σ = 40 minutes. The number of observations required is closest to:

1180.
683.
482.
22.

Answer 1

Answer: 482

Explanation:

Formula to find the sample size is given by :-

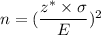`n= ((z^** \sigma)/(E))^2` (1)

, where z* = critical z-value (two tailed).

`\sigma` = Population standard deviation and E = Margin of error.

As per given , we have

Margin of error : E= 3

`\sigma=40`

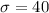
Confidence level = 90%

Significance level =
`\alpha=1-0.90=0.10`

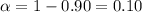
Using z-table , the critical value for 90% confidence=
`z^*=z_(\alpha/2)=z_(0.05)=1.645`

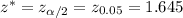
Required minimum sample size =
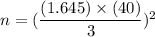`n= (((1.645)* (40))/(3))^2` [Substitute the values in formula (1)]

`n=(21.9333333333)^2`

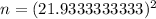
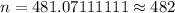`n=481.07111111\approx482` [ Round to the next integer]

Hence, the number of observations required is closest to 482.