Question

Flywheels are large, massive wheels used to store energy. They can be spun up slowly, then the wheels energy can be released quickly to accomplish a task that demands high power. An industrial flywheel has a 1.5 m diameter and a mass of 250 kg.

1. A motor spins up the flywheel with a constant torque of 50 N*m. How long does it take the flywheel to reach top angular speed of 1200 rpm
2. How much energy is stored in the flywheel?

Answer 1

176.99113 seconds

555165.24756 J

Step-by-step explanation:

d = Diameter of wheel = 1.5 m

r = Radius =
`(d)/(2)=(1.5)/(2)=0.75\ m`

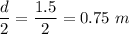
m = Mass of wheel = 250 kg

`\tau` = Torque = 50 Nm

`\omega` = Angular speed = 1200 rpm

Moment of inertia is given by

`I=(1)/(2)mr^2\\\Rightarrow I=(1)/(2)250* 0.75^2\\\Rightarrow I=70.3125\ kgm^2`

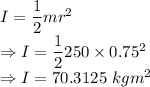
Angular acceleration is given by

`\alpha=(\tau)/(I)\\\Rightarrow \alpha=(50)/(70.3125)\\\Rightarrow \alpha=0.71\ rad/s^2`

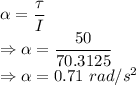
Time taken is given by

`t=(\omega)/(\alpha)\\\Rightarrow t=(1200* (2\pi)/(60))/(0.71)\\\Rightarrow t=176.99113\ s`

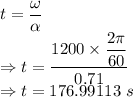
The time it takes for the flywheel to reach top angular speed is 176.99113 seconds

Kinetic energy is given by

`K=(1)/(2)I\omega^2\\\Rightarrow K=(1)/(2)70.3125* (1200* (2\pi)/(60))^2\\\Rightarrow K=555165.24756\ J`

The energy is stored in the flywheel is 555165.24756 J