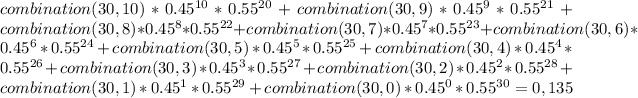Question

In a certain large city, 45% of families earn less than $35,000 per year. Assuming the distribution is binomial and you can use the exact binomial calculation, what's the probability, accurate to the number of decimal places given, that a simple random sample of 30 families will have 10 or fewer families earning less than $35,000 per year? Use the exact binomial calculation.

Answer 1

The probability is %13,5

Explanation:

If it is a binomial distribution function than we can find a probability of earning less or more than 35000$ in this certain large city. Lets assume that p is probability of earning less than 35000$ and q is earning more than 35000$.:

p=0,45

q=0,55

So general formula of n families that earning less than 35000$ is:

`P(X=n)=combination(30,n)*0,45^n*0,55^(30-n)`

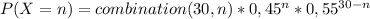
Probability of 10 or less families out of 30 families that earning less than 35000$ is:

`combination(30,10)*0.45^(10)*0.55^(20)+combination(30,9)*0.45^9*0.55^(21)+combination(30,8)*0.45^8*0.55^(22)+combination(30,7)*0.45^7*0.55^(23)+combination(30,6)*0.45^6*0.55^(24)+combination(30,5)*0.45^5*0.55^(25)+combination(30,4)*0.45^4*0.55^(26)+combination(30,3)*0.45^3*0.55^(27)+combination(30,2)*0.45^2*0.55^(28)+combination(30,1)*0.45^(1)*0.55^(29)+combination(30,0)*0.45^0*0.55^(30)=0,135`