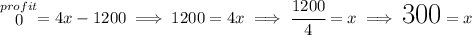Question

How many widgets does Widget INC. have to sell to break even?

Answer 1

well, we know the table has linear relationship, so let's use it to get the Profit function then, to get the equation of any straight line, we simply need two points off of it, so let's use those two points in the picture below.

`(\stackrel{x_1}{500}~,~\stackrel{y_1}{800})\qquad (\stackrel{x_2}{700}~,~\stackrel{y_2}{1600}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{1600}-\stackrel{y1}{800}}}{\underset{run} {\underset{x_2}{700}-\underset{x_1}{500}}} \implies \cfrac{1600 -800}{700 -500} \implies \cfrac{ 800 }{ 200 }\implies 4`

`\begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{800}=\stackrel{m}{4}(x-\stackrel{x_1}{500}) \\\\\\ y-800=4x-2000\implies y=4x-1200`

how many bucks will they lose by selling "0" items?

well, let's find out by setting x = 0.

`\stackrel{profit}{y}=4(0)-1200\implies y=-1200~\hfill \stackrel{\textit{they'd be losing}}{\text{\LARGE 1200}}`

how many will they need to sell to break-even?

well, to break-even that means no loses, no profits but no loses either, so-called breaking-even, you simply sell enough to cover costs, at that point the profit = y = 0, so

`\stackrel{profit}{0}=4x-1200\implies 1200=4x\implies \cfrac{1200}{4}=x\implies \text{\LARGE 300}=x`

Answer 2

300 widgets

Explanation:

Each time the widgets sold goes up by 100, the profits goes up by 400. This shows a ratio/slope of 4 if we were to graph this. To find out when they break even you need to subtract $400 from the first row to get to zero and the equivalent amount of widgets. If each widget is $4 then subtract 100 from 400 to get 300 widgets