Question

As part of a science project you investigate the effect of punching holes in a plastic container of water and observing the flow of liquid out of the different holes. If the container has a water level 20 cm above the base and you punch a hole in the side 12 cm high, calculate the speed at which water will initially flow out of the hole.

a.1.25 m/s
b.15.3 m/s
c.12.5 m/s
d. 1.50 m/s

Answer 1

The speed at which water will initially flow out of the hole is 12.5 m/s.

Step-by-step explanation:

It is given that,

The water level in the container, h = 20 cm

Height of the hole above ground, h' = 12 cm

We need to find the speed at which water will initially flow out of the hole. It can be calculated using the conservation of energy. It is given by equation the kinetic energy gained and the potential energy lost.

`v=√(2gH)`

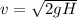
H = h - h'

H = 20 cm - 12 cm = 8 cm

`v=√(2* 9.8\ m/s^2* 8\ m)`

v = 12.52 m/s

or

v = 12.5 m/s

So, the speed at which water will initially flow out of the hole is 12.5 m/s. Hence, this is the required solution.