Answer:
The Annual rate of interest for the mortgage is 1.8%
Explanation:
Given as :
The mortgage principal = p = $167,000
The time period of mortgage = t = 20 years
The Amount paid towards mortgage in 20 years = A = $240,141
Let the Annual percentage rate on interest = r % compounded annually
Now, From Compound Interest method
Amount = Principal ×
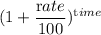
Or, A = p ×
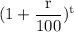
Or, $240,141 = $167,000 ×
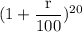
or,
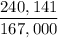 =
=
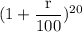
Or , 1.437 =
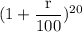
Or,
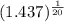 =
=
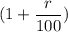
or, 1.018 =
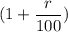
Or,
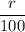 = 1.018 - 1
= 1.018 - 1
Or,
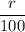 = 0.018
= 0.018
∴ r = 0.018 × 100
i.e r = 1.8
So, The rate of interest applied = r = 1.8 %
Hence, The Annual rate of interest for the mortgage is 1.8% Answer