Answer:
A bowling ball (8.21rad/s) > A tire (7.94rad/s) > A square (7.75rad/s) > A rock (6.98rad/s) > A top spinning (6.54rad/s)
Explanation:
To rank the angular speed (ω) of the objects, we need first calculate its value for every object:
A bowling ball of radius 12.3cm rotating at 8.21 radians per second:
ω = 8.21 rad/s
A tire of radius 0.321m rotating at 75.8 rpm:
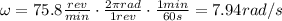
A 6.84cm diameter top spinning at 375 degrees per second:
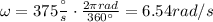
A square with sides (b) 0.458m long, whose corners are moving with tangential speed (v) 2.51 m/s as it rotates about its center:
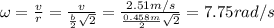
A rock on a string, being swung in a circle of radius 0.521 m with a centripetal acceleration (a) of 25.4 m/s²:
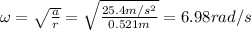
Now, the rank of the angular speed of the objects, from highest to lowest is:
A bowling ball (8.21rad/s) > A tire (7.94rad/s) > A square (7.75rad/s) > A rock (6.98rad/s) > A top spinning (6.54rad/s)
I hope it helps you!