Answer:

Explanation:
This is a "power" raised to another "power" problem. Lets see the rule of exponents that dictates solving this type of problem.
Power rule of Exponents:
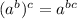
We basically multiply the powers together. So this problem becomes:
![[3^(-2)]^4=3^(-2*4)=3^(-8)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/753nrrp5sgluuyfb5jrp9acbfgl7h2hdou.png)
We can use another property to make it simpler. The property is:
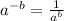
So, the problem becomes:
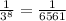
In fractional form, this is the answer:
