Answer:
The expected value is 1.8
Explanation:
Consider the provided information.
Suppose there’s a 15% chance of having 0 announcements, a 30% chance of having 1 announcement, a 25% chance of having 2 announcements, a 20% chance of having 3 announcements, and a 10% chance of having 4 announcements.
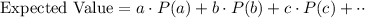
Where a is the announcements and P(a) is the probability.


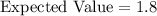
Hence, the expected value is 1.8