Question

If the coefficient of static friction between tires and pavement is 0.60, calculate the minimum torque that must be applied to the 69-cm-diameter tire of a 920-kg automobile in order to "lay rubber" (make the wheels spin, slipping as the car accelerates). Assume each wheel supports an equal share of the weight.

Answer 1

To solve this problem, it is necessary to apply the definitions and concepts related to Newton's second law, which relate the variables of the Normal Force, Weight, friction force and finally the Torque.

We start under the definition that the Normal Force of one of the 4 tires of the car would be subject to

`N = (mg)/(4)`

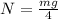
Where,

m = mass

g = Gravitational Acceleration

Therefore the Normal Force of each wheel would be

`N = (920*9.8)/(4)`

`N =  2254N`

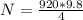
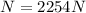
Now the friction force can be determined as

`f_s = \mu_s N`

`f_s = 0.60 * 2254`

`f_s = 1352.4N`

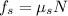
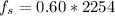
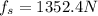
The radius of each of the tires is given as

`r = (69)/(2)`

`r = 34.5cm = 0.345m`

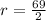
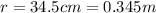
Finally, the torque is made between the friction force (which is to be overcome) and the radius of each of the wheels, therefore:

`\tau = r*f_s`

`\tau = (0.345)(1352.4)`

`\tau = 466.578N\cdot m`

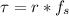
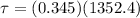
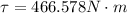
Therefore the engine of the car must apply a torque of about
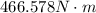`466.578N\cdot m` to lay rubber