1 Answer

NgocLK · Answer 1 · 2020-11-09T09:01:54+0000

Answer with explanation:

When the sample size is small (< 30) and the population standard deviation is unknown , then we use t-test.

The confidence interval for population mean will be :

$\overline{x}\pm t^*(s)/(√(n))$ (1)

, where
$\overline{x}$ = sample mean

t* = Critical value (based on degree of freedom and significance level).

s= sample standard deviation

n= sample size.

As per given we have

n= 9

Degree of freedom = n-1 = 8

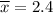
$\overline{x}=2.4$

s= 0.75

Significance level =
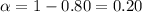
$\alpha=1-0.80=0.20$

Using students' t distribution table ,

Critical value :
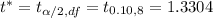
$t^*=t_(\alpha/2,df)=t_(0.10,8)=1.3304$

We assume that the population is approximately normal.

Then, a 80% confidence interval for the mean waste recycled per person per day for the population of Florida will be :

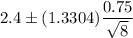$2.4\pm (1.3304)(0.75)/(√(8))$ (Substitute the values in (1))

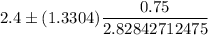
$2.4\pm (1.3304)(0.75)/(2.82842712475)$

$2.4\pm (1.3304)(0.265165042945)$

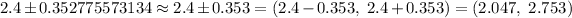
$2.4\pm 0.352775573134\approx2.4\pm0.353=(2.4-0.353,\ 2.4+0.353)=(2.047,\ 2.753)$

Hence, the 80% confidence interval for the mean waste recycled per person per day for the population of Florida. = (2.047, 2.753)