Answer with explanation:
When the sample size is small (< 30) and the population standard deviation is unknown , then we use t-test.
The confidence interval for population mean will be :
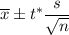 (1)
(1)
, where
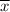 = sample mean
= sample mean
t* = Critical value (based on degree of freedom and significance level).
s= sample standard deviation
n= sample size.
As per given we have
n= 9
Degree of freedom = n-1 = 8
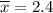
s= 0.75
Significance level =
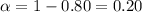
Using students' t distribution table ,
Critical value :
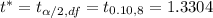
We assume that the population is approximately normal.
Then, a 80% confidence interval for the mean waste recycled per person per day for the population of Florida will be :
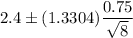 (Substitute the values in (1))
(Substitute the values in (1))
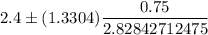
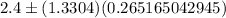
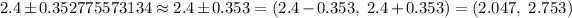
Hence, the 80% confidence interval for the mean waste recycled per person per day for the population of Florida. = (2.047, 2.753)