Question

The volume of soda a dispensing machine pours into a 12-ounce can of soda follows a normal distribution with a mean of 12.45 ounces and a standard deviation of 0.30 ounce. The company receives complaints from consumers who actually measure the amount of soda in the cans and claim that the volume is less than the advertised 12 ounces. What proportion of the soda cans contain less than the advertised 12 ounces of soda?

Answer 1

Answer: 0.0668

Explanation:

Given : The volume of soda a dispensing machine pours into a 12-ounce can of soda follows a normal distribution with a mean of 12.45 ounces and a standard deviation of 0.30 ounce.

i.e.
`\mu=12.45` and
`\sigma=0.30`

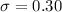
Let x denotes the volume of soda a dispensing machine pours into a 12-ounce can.

Then, the proportion of the soda cans contain less than the advertised 12 ounces of soda will be :-

`P(x<12)=P((x-\mu)/(\sigma)<(12-12.45)/(0.30))\\\\=P(z<-1.5)\ \ [\because z=(x-\mu)/(\sigma)]\\\\=1-P(z<1.5)\ \ [\because P(Z<-z)=1-P(Z<z)]\\\\=1-0.9332\ [\text{By z-table}]\\\\=0.0668`

Hence, the proportion of the soda cans contain less than the advertised 12 ounces of soda = 0.0668