Question

Starting from rest, Christina experiences 24.5 m/s2 of acceleration to take off from an aircraft carrier for 5 seconds. How long does the runway need to be? Round to the nearest meter.

Answer 1

The length of the runway to the nearest meter is 306 m.

Step-by-step explanation:

Given:

Initial velocity of Christina is,
`u=0\ m/s(Rest)`

Time taken is,
`t=5\ s`

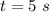
Acceleration experienced by Christina is,
`a=24.5\ m/s^2`

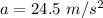
The length of the runway is,
`d=?`

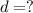
Now, we use Newton's equation of motion that relates the distance, initial velocity, time and acceleration.

So, we have the following equation of motion:

`d=ut+(1)/(2)at^2`

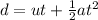
Plug in all the given values and solve for 'd'. This gives,

`d=0+(1)/(2)* 24.5* 5^2\\\\d=(1* 24.5* 25)/(2)\\\\d=(612.5)/(2)\\\\d=306.25\approx 306\ m(\textrm{Rounding to nearest meter})`

Therefore, the length of the runway to the nearest meter is 306 m.