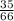Answer:
a)
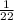
b)
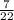
c)
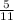
d)
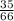
Explanation:
Given,
Number of blue socks = 4,
Grey socks = 5,
Black socks = 3,
Total socks = 4 + 5 + 3 = 12,
Ways of choosing any 2 socks =
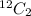
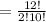
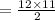
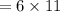
= 66,
a) Ways of choosing 2 blue socks =
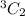
= 3,
Since,

Thus, the probability of selecting 2 blue socks =
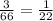
b) Ways of choosing 2 shocks, non of them are grey socks =

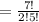
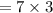
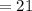
Thus, the probability of selecting no grey socks =
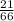
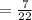
c) ways of selecting atleast 1 black sock = ways of selecting 1 black sock + ways of selecting 2 black socks
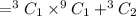

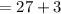
= 30,
Thus, the probability of selecting at least 1 black sock =
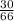
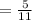
d) Ways of selecting a green sock =
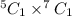
= 35,
Thus, the probability of selecting a green sock =