Question

81. A 560-g squirrel with a surface area of 930cm2 falls from a 5.0-m tree to the ground. Estimate its terminal velocity. (Use a drag coefficient for a horizontal skydiver.) What will be the velocity of a 56-kg person hitting the ground, assuming no drag contribution in such a short distance?

Answer 1

(a). The terminal velocity is 9.83 m/s.

(b). The velocity is 9.9 m/s.

Step-by-step explanation:

Given that,

Mass of squirrel = 560 g

Surface area = 930 cm²

Height = 5.0 m

Weight of person = 56 kg

We need to calculate the terminal velocity

Using formula of terminal velocity

`v_(t)=\sqrt{(2mg)/(\rho A C_(d))}`

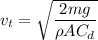
Where, A = area

`\rho` = density

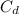`C_(d)` = drag coefficient

m = mass

Put the value into the formula

`v_(t)=\sqrt{(2*0.560*9.8)/(1.22*0.093*1)}`

`v_(t)=9.83\ m/s`

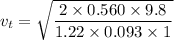
The terminal velocity is 9.83 m/s.

We need to calculate the velocity

Using equation of motion

`v^2=u^2+2gs`

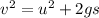
Put the value into the formula

`v=√(2* 9.8*5)`

`v=9.9\ m/s`

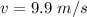
Hence, (a). The terminal velocity is 9.83 m/s.

(b). The velocity is 9.9 m/s.

Answer 2

Step-by-step explanation:

Given

mass of squirrel
`m=560 gm`

Surface area of squirrel
`A=930 cm^2`

and the area which face
`A_f=(A)/(2)=465 cm^2`

height of tree
`h=5 m`

Coefficient of drag
`C=1`

drag Force
`F_d=(1)/(2)C\cdot \rho \cdot A\cdot v^2`

Terminal velocity is given

`F_d=mg`

`(1)/(2)C\cdot \rho \cdot A\cdot v^2=mg`

`v=\sqrt{(2* m* g)/(\rho * C* A_f)}`

`v=\sqrt{(2* 0.560* 9.8)/(1.2* 1* 465* 10^(-4))}`

`v=13.9 m/s`

(b)Mass of person
`m=56 kg`

`v^2-u^2=2gh`

`u=0`

`v=√(2gh)`

`v=√(2* 9.8* 5)`

`v=9.89 m/s`