Answer: The maximum error = $105.76.
Explanation:
Formula to find the maximum error:
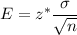
, where n= sample size.
 = Population standard deviation
= Population standard deviation
z*= Critical value(two-tailed).
As per given , we have
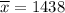
n= 35
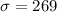
For 98% confidence , the significance level =
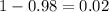
By z-table , the critical value (two -tailed) =
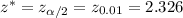
Now , the maximum error =
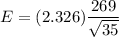

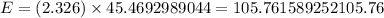
Hence, With 98% confidence level , the maximum error = $105.76.