Question

Dolomite is a mixed carbonate of calcium and magnesium. Calcium and magnesium carbonates both decompose upon heating to produce the metal oxides (MgO and CaO) and carbon dioxide (CO2). If 4.84 g of residue consisting of MgO and CaO remains when 9.66 g of dolomite is heated until decomposition is complete, what percentage by mass of the original sample was MgCO3?

Answer 1

72.03 %

Step-by-step explanation:

Total mass of dolomite = 9.66 g

Let the mass of Magnesium carbonate = x g

The mass of calcium carbonate = 9.66 - x g

Calculation of the moles of Magnesium carbonate as:-

Molar mass of Magnesium carbonate = 122.44 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

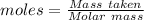
Thus,

`Moles= (x\ g)/(84.3139\ g/mol)=(x)/(84.3139)\ mol`

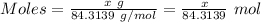
Calculation of the moles of calcium carbonate as:-

Molar mass of calcium carbonate = 100.0869 g/mol

Thus,

`Moles= (9.66 - x\ g)/(100.0869\ g/mol)=(9.66 - x)/(100.0869)\ mol`

According to the reaction shown below:-

`MgCO_3\rightarrow MgO+CO_2`

`CaCO_3\rightarrow CaO+CO_2`

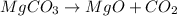
In both the cases, the oxides formed from the carbonates in the 1:1 ratio.

So, Moles of MgO =
`(x)/(84.3139)\ mol`

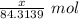
Molar mass of MgO = 40.3044 g/mol

Thus, Mass = Moles*Molar mass =
`(x)/(84.3139)* 40.3044 \ g`

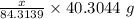
Moles of CaO =
`(9.66 - x)/(100.0869)\ mol`

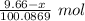
Molar mass of CaO = 56.0774 g/mol

Thus, Mass = Moles*Molar mass =
`(9.66 - x)/(100.0869)* 56.0774 \ g`

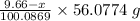
Given that total mass of the oxide = 4.84 g

Thus,

`(x)/(84.3139)* 40.3044 +(9.66 - x)/(100.0869)* 56.0774=4.84`

`(40.3044x)/(84.3139)+56.0774* (-x+9.66)/(100.0869)=4.84`

`-694.1618435x+45673.48749\dots =40843.38968\dots`

`x=(4830.09780\dots )/(694.1618435)`

`x=6.9582`

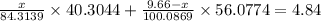
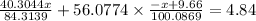
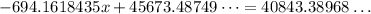
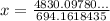
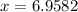
Thus, the mass of Magnesium carbonate = 6.9582 g

`\%\ mass=(Mass_(MgCO_3))/(Total\ mass)* 100`

`\%\ mass=(6.9582)/(9.66)* 100=72.03\ \%`