Question

3. Which polynomial is equal to

(-3x2 + 2x - 3) subtracted from
(x3 - x² + 3x)?

A 2x² + 2x² + x -
B-2x² + 2x² + x + 3
C x² + 2x² +
x3
Dx² + 2? + x + 3
X

Answer 1

Which polynomial is equal to (-3x^2 + 2x - 3) subtracted from (x^3 - x^2 + 3x)?

Answer:

The polynomial equal to (-3x^2 + 2x - 3) subtracted from (x^3 - x^2 + 3x) is
`x^3 + 2x^2 + x + 3`

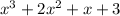
Solution:

Given that two polynomials are:
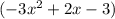`(-3x^2 + 2x - 3)` and
`(x^3 - x^2 + 3x)`

We have to find the result when
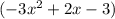`(-3x^2 + 2x - 3)` is subtracted from
`(x^3 - x^2 + 3x)`

In basic arithmetic operations,

when "a" is subtracted from "b" , the result is b - a

Similarly,

When
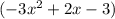`(-3x^2 + 2x - 3)` is subtracted from
`(x^3 - x^2 + 3x)` , the result is:

`\rightarrow (x^3 - x^2 + 3x) - (-3x^2 + 2x - 3)`

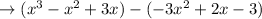
Let us solve the above expression

There are two simple rules to remember:

• When you multiply a negative number by a positive number then the product is always negative.

• When you multiply two negative numbers or two positive numbers then the product is always positive.

So the above expression becomes:

`\rightarrow (x^3 - x^2 + 3x) + 3x^2 -2x + 3`

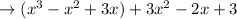
Removing the brackets we get,

`\rightarrow x^3 - x^2 + 3x + 3x^2 -2x + 3`

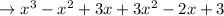
Combining the like terms,

`\rightarrow x^3 -x^2 + 3x^2 + 3x - 2x + 3`

`\rightarrow x^3 + 2x^2 + x + 3`

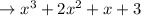
Thus the resulting polynomial is found