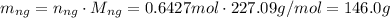Question

Nitroglycerin is a dangerous powerful explosive that violently decomposes when it is shaken or dropped. The Swedish chemist Alfred Nobel (1833-1896) founded the Nobel Prizes with a fortune he made by inventing dynamite, a mixture of nitroglycerin and inert ingredients that was safe to handle. (1) Write a balanced chemical equation, including physical state symbols, for the decomposition of liquid nitroglycerin ( C3H5NO33 ) into gaseous dinitrogen, gaseous dioxygen, gaseous water and gaseous carbon dioxide. (2) Suppose 41.0L of carbon dioxide gas are produced by this reaction, at a temperature of −14.0°C and pressure of exactly 1atm . Calculate the mass of nitroglycerin that must have reacted. Round your answer to 3 significant digits.

Answer 1

a.
`4 C_3H_5N_3O_9 (l)\rightarrow 6N_2 (g) + O_2 (g) + 10 H_2O (g) + 12 CO_2 (g)`

b. 146.0 g

Step-by-step explanation:

Question 1 (a). Just as the problem states, liquid nitroglycerin decomposes into nitrogen gas
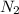`N_2`, oxygen gas
`O_2`, water vapor
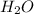`H_2O` and carbon dioxide
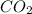`CO_2`. Let's write the decomposition of nitroglycerin into these 4 components:

`C_3H_5N_3O_9 (l)\rightarrow N_2 (g) + O_2 (g) + H_2O (g) + CO_2 (g)`

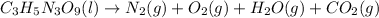
Now we need to balance the equation. Firstly, notice we have 3 carbon atoms on the left and 1 on the right, so let's multiply carbon dioxide by 3:

`C_3H_5N_3O_9 (l)\rightarrow N_2 (g) + O_2 (g) + H_2O (g) + 3 CO_2 (g)`

Now, we have 3 nitrogen atoms on the left and 2 on the right, so let's multiply nitrogen on the right by
`(3)/(2)`:

`C_3H_5N_3O_9 (l)\rightarrow (3)/(2)N_2 (g) + O_2 (g) + H_2O (g) + 3 CO_2 (g)`

We have 5 hydrogen atoms on the left, 2 on the right, so let's multiply the right-hand side by
`(5)/(2)`:

`C_3H_5N_3O_9 (l)\rightarrow (3)/(2)N_2 (g) + O_2 (g) + (5)/(2) H_2O (g) + 3 CO_2 (g)`

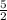Finally, count the oxygen atoms. We have a total of 9 on the left. On the right we have (excluding oxygen molecule):

`(5)/(2) + 6 = 8.5`

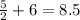
This leaves
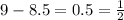`9 - 8.5 = 0.5 = (1)/(2)` of oxygen. Since oxygen is diatomic, we need to take one fourth of it to get one half in total:

`C_3H_5N_3O_9 (l)\rightarrow (3)/(2)N_2 (g) + (1)/(4) O_2 (g) + (5)/(2) H_2O (g) + 3 CO_2 (g)`

To make it look neater without fractional coefficients, multiply both sides by 4:

`4 C_3H_5N_3O_9 (l)\rightarrow 6N_2 (g) + O_2 (g) + 10 H_2O (g) + 12 CO_2 (g)`

Question 2 (b). Now we can make use of the balanced chemical equation and apply it for the context of this separate problem. We're given the following variables:

`V_(CO_2) = 41.0 L`

`T = -14.0^oC + 273.15 K = 259.15 K`

`p = 1 atm`

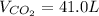
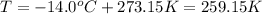
Firstly, we may find moles of carbon dioxide produced using the ideal gas law
`pV = nRT`.

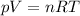Rearranging for moles, that is, dividing both sides by RT (here R is the ideal gas law constant):

`n_(CO_2) = (pV_(CO_2))/(RT) = (1 atm\cdot 41.0 L)/(0.08206 (L atm)/(mol K)\cdot 259.15 K) = 1.928 mol`

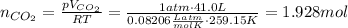
According to the stoichiometry of the balanced chemical equation:

`4 C_3H_5N_3O_9 (l)\rightarrow 6N_2 (g) + O_2 (g) + 10 H_2O (g) + 12 CO_2 (g)`

4 moles of nitroglycerin (ng) produce 12 moles of carbon dioxide. From here we can find moles o nitroglycerin knowing that:

`(n_(ng))/(4) = (n_(CO_2))/(12) \therefore n_(ng) = (4)/(12)n_(CO_2) = (1)/(3)\cdot 1.928 mol = 0.6427 mol`

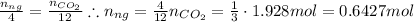
Multiplying the number of moles of nitroglycerin by its molar mass will yield the mass of nitroglycerin decomposed:

`m_(ng) = n_(ng)\cdot M_(ng) = 0.6427 mol\cdot 227.09 g/mol = 146.0 g`