Question

Use the exponential decay​ model, Upper A equals Upper A 0 e Superscript kt​, to solve the following. The​ half-life of a certain substance is 19 years. How long will it take for a sample of this substance to decay to 78​% of its original​ amount? It will take approximately nothing years for the sample of the substance to decay to 78​% of its original amount.

Answer 1

It will take 7 years ( approx )

Explanation:

Given equation that shows the amount of the substance after t years,

`A=A_0 e^(kt)`

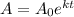
Where,

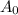`A_0` = Initial amount of the substance,

If the half life of the substance is 19 years,

Then if t = 19, amount of the substance =
`(A_0)/(2)`,

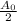i.e.

`(A_0)/(2)=A_0 e^(19k)`

`(1)/(2) = e^(19k)`

`0.5 = e^(19k)`

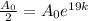
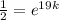
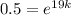
Taking ln both sides,

`\ln(0.5) = \ln(e^(19k))`

`\ln(0.5) = 19k`

`\implies k = (\ln(0.5))/(19)\approx -0.03648`

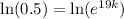
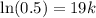
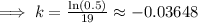
Now, if the substance to decay to 78​% of its original​ amount,

Then
`A=78\% \text{ of }A_0 =(78A_0)/(100)=0.78 A_0`

`0.78 A_0=A_0 e^(-0.03648t)`

`0.78 = e^(-0.03648t)`

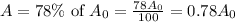
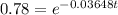
Again taking ln both sides,

`\ln(0.78) = -0.03648t`

`-0.24846=-0.03648t`

`\implies t = (0.24846)/(0.03648)=6.81085\approx 7`

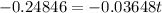
Hence, approximately the substance would be 78% of its initial value after 7 years.