Answer:
35 revolutions
Step-by-step explanation:
t = Time taken
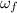 = Final angular velocity
= Final angular velocity
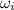 = Initial angular velocity
= Initial angular velocity
 = Angular acceleration
= Angular acceleration
 = Number of rotation
= Number of rotation
Equation of rotational motion
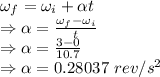
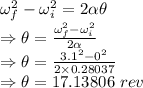
Number of revolutions in the 10.7 seconds is 17.13806
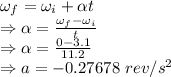
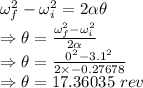
Number of revolutions in the 11.2 seconds is 17.36035
Total total number of revolutions in the 21.9 second interval is 17.13806+17.36035 = 34.49841 = 35 revolutions