A circle centered at
 with radius
with radius
 (the length of
(the length of
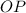 ) has equation
) has equation
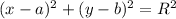
which can be parameterized by
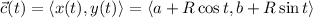
with
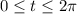 .
.
The tangent line to
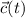 at a point
at a point
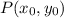 is
is
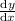 with
with
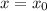 and
and
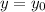 . By the chain rule (and this is where we use implicit differentiation),
. By the chain rule (and this is where we use implicit differentiation),
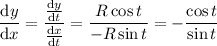
At the point
 , we have
, we have


so that the slope of the line tangent to the circle at
 is
is
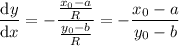
Meanwhile, the slope of the line through the center
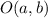 and the point
and the point
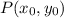 is
is
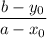
Recall that perpendicular lines have slopes that are negative reciprocals of one another; taking the negative reciprocal of this slope gives
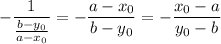
which is exactly the slope of the tangent line.