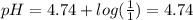Answer:
A: pH = 3.74
B: pH = 5.74
C: pH = 4.74
Step-by-step explanation:
According to the Henderson-Hasselbach equation for buffers, we know that
![pH = pK_a + log(([A^-])/([HA]))](https://img.qammunity.org/2020/formulas/chemistry/high-school/siqawk6rs4wewieoopscqovyk39ltyoqs5.png) . Firstly, let's find the
. Firstly, let's find the
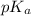 value:
value:
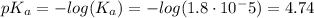
Now, for buffer A:
![([A^-])/([HA])=([CH_3COO^-])/([CH_3COOH])=(1)/(10)](https://img.qammunity.org/2020/formulas/chemistry/high-school/xq3gyfm0urpp2myhsulczp6l3swapy07ch.png)
This means:
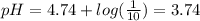
Similarly, for buffer B:
![([A^-])/([HA])=([CH_3COO^-])/([CH_3COOH])=(10)/(1)](https://img.qammunity.org/2020/formulas/chemistry/high-school/bkhykm9pnheuigzkto2928otc8ztpr8k2p.png)
This means:
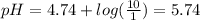
Similarly, for buffer C:
![([A^-])/([HA])=([CH_3COO^-])/([CH_3COOH])=(1)/(1)](https://img.qammunity.org/2020/formulas/chemistry/high-school/obw7tts4yaq6rv51bm56xlrn4mg48r0d3k.png)
This means: