Answer: 38.41 minutes
Explanation:
The standard error for the difference in means is given by :-
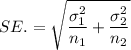
where ,
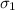 = Standard deviation for sample 1.
= Standard deviation for sample 1.
 = Size of sample 1.
= Size of sample 1.
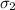 = Standard deviation for sample 2.
= Standard deviation for sample 2.
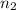 = Size of sample 2.
= Size of sample 2.
Let the sample of Latino name is first and non -Latino is second.
As per given , we have
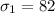
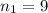
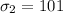
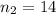
The standard error for the difference in means will be :
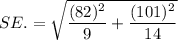
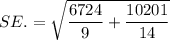
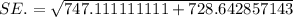
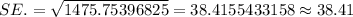
Hence, the standard error for the difference in means =38.41 minutes