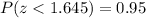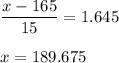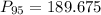Question

Q6. (15 points) IQ examination scores of 500 members of a club are normally distributed with mean of 165 and SD of 15.

(a) What is the probability that the members of the club have IQ scores at most 180?
(b) How many of the members of the club have IQ scores at most 180?
(c) Find and interpret P95 -the 95-th percentile.

Answer 1

a) 0.8413

b) 421

c)
`P_(95) = 189.675`

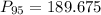
Explanation:

We are given the following information in the question:

Mean, μ = 165

Standard Deviation, σ = 15

We are given that the distribution of IQ examination scores is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

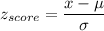
a) P(IQ scores at most 180)

P(x < 180)

`P( x < 180) = P( z < \displaystyle(180 - 165)/(15)) = P(z < 1)`

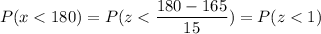
Calculation the value from standard normal z table, we have,

`P(x < 180) = 0.8413 = 84.13\%`

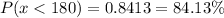
b) Number of the members of the club have IQ scores at most 180

n = 500

`\text{Members} = n* \text{P(IQ scores at most 180)}\\= 500* 0.8413\\=420.65 \approc 421`

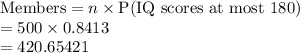
c) P(X< x) = 0.95

We have to find the value of x such that the probability is 0.95

`P( X < x) = P( z < \displaystyle(x - 165)/(15))=0.95`

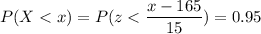
Calculation the value from standard normal z table, we have,

`P(z < 1.645) = 0.95`

`\displaystyle(x - 165)/(15) = 1.645\\\\x = 189.675`

`P_(95) = 189.675`