Answer:
 = 96
= 96

Explanation:
The n th term of a geometric sequence is
 = a
= a

where a is the first term and r the common ratio.
Both values have to be found.
Using
a₂ = - 144, then
ar = - 144 → (1)
a₅ = 486, then
a
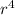 = 486 → (2)
= 486 → (2)
Divide (2) by (1)
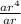 =
=
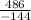
r³ = - 3.375 ( take the cube root of both sides )
r = - 1.5
Substitute r = - 1.5 into (1)
- 1.5a = - 144 ( divide both sides by - 1.5 )
a = 96
Hence explicit formula is
 = 96
= 96
