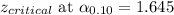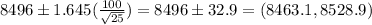Question

On the basis of extensive tests, the yield point of a particular type of mild steel-reinforcing bar is known to be normally distributed with σ = 100. The composition of the bar has been slightly modified, but the modification is not believed to have affected either the normality or the value of σ. (a) Assuming this to be the case, if a sample of 25 modified bars resulted in a sample average yield point of 8496 lb, compute a 90% CI for the true average yield point of the modified bar. (Round your answers to one decimal place.)

Answer 1

90% Confidence interval: (8463.1,8528.9)

Explanation:

We are given the following in the question:

Sample mean,
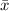`\bar{x}` = 8496 lb

Sample size, n = 125

Alpha, α = 0.10

Population standard deviation, σ = 100

90% Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

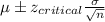
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.10) = 1.645`

`8496 \pm 1.645((100)/(√(25)) ) = 8496 \pm 32.9 = (8463.1,8528.9)`