Question

A 84.5 kg astronaut is working on the engines of a spaceship that is drifting through space with a constant velocity. The astronaut turns away to look at Earth and several seconds later is 38.9 m behind the ship, at rest relative to the spaceship. The only way to return to the ship without a thruster is to throw a wrench directly away from the ship. The wrench has a mass of 0.613 kg, and the astronaut throws the wrench with a speed of 24.9 m/s. How long does it take the astronaut to reach the ship? Answer in units of s.

Answer 1

215.35736 seconds

Step-by-step explanation:

`m_1` = Mass of astronaut = 84.5 kg

`m_2` = Mass of wrench = 0.613 kg

`v_1` = Velocity of astronaut

`v_2` = Velocity of wrench = 24.9 m/s

In this system the linear momentum is conserved

`m_1v_1=m_2v_2\\\Rightarrow v_1=(m_2v_2)/(m_1)\\\Rightarrow v_1=(0.613* 24.9)/(84.5)\\\Rightarrow v_1=0.18063\ m/s`

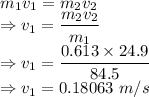
Time is given by

`Time=(Distance)/(Speed)`

`Time=(38.9)/(0.18063)=215.35736\ s`

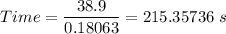
The time it will take the astronaut to get back to the ship is 215.35736 seconds