Question

A flat, circular, metal loop of radius r = 1 m is at rest in a uniform magnetic field of magnitude B. The plane of the loop is parallel to the page and the magnetic field is directed perpendicular to and out of the page, as indicated by the blue dots. If the magnitude of the magnetic field increases from 2 T to 6 T in 2 s, what is the magnitude of the induced emf within the circular loop?

Answer 1

Induced EMF,
`\epsilon=6.28\ volts`

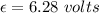
Step-by-step explanation:

Given that,

Radius of the circular loop, r = 1 m

Time, t = 2 s

Initial magnetic field,
`B_i=2\ T`

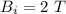
Final magnetic field,
`B_f=6\ T`

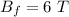
The expression for the induced emf within the circular loop is given by :

`\epsilon=(d\phi)/(dt)`

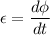
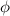`\phi` = magnetic flux

`\epsilon=(d(BA\ cos\theta))/(dt)`

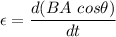
Here,
`\theta=90\ degrees`

`\epsilon=A(d(B))/(dt)`

`\epsilon=A(B_f-B_i)/(t)`

`\epsilon=\pi (1)^2* (6-2)/(2)`

`\epsilon=6.28\ volts`

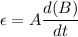
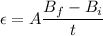
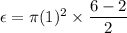
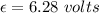
So, the induced emf in the loop is 6.28 volts. Hence, this is the required solution.