Question

A huge cannon is assembled on an airless planet (ignore any effects due to the planet's rotation). The planet has a radius of 5.00 × 106 m and a mass of 3.95 × 1023 kg. The cannon fires a projectile straight up at 2000 m/s. An observation satellite orbits the planet at a height of 1000 km. What is the projectile's speed as it passes the satellite?

Answer 1

The projectile's speed as it passes the satellite is 1497.8 m/s.

Step-by-step explanation:

Given that,

Radius of planet
`r=5.00*10^(6)\ m`

Mass of planet
`m=3.95*10^(23)\ kg`

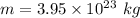
Speed = 2000 m/s

Height = 1000 km

We need to calculate the projectile's speed as it passes the satellite

Using conservation of energy

`E_(1)=E_(2)`

`(1)/(2)mv_(1)^2+(GmM)/(r_(1))=(1)/(2)mv_(2)^2+(GmM)/(R+h)`

`(v_(1)^2)/(2)+(GM)/(r_(1))=(v_(2)^2)/(2)+(GM)/(R+h)`

`-(v_(2)^2)/(2)=-((GM)/(R)-(GM)/(R+h)-(v_(1)^2)/(2))`

`v_(2)^2=v_(1)^2+2GM((1)/(R+h)-(1)/(R))`

`v_(2)=\sqrt{v_(1)^2+2GM((1)/(R+h)-(1)/(R))}`

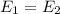
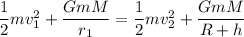
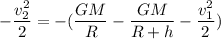
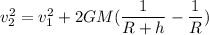
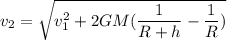
Put the value into the formula

`v_(2)=\sqrt{2000^2+2*6.67*10^(-11)*3.95*10^(23)((1)/(5.00*10^(6)+1000*10^(3))-(1)/(5.00*10^(6)))}`

`v_(2)=1497.8\ m/s`

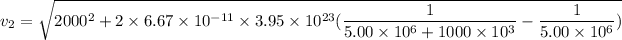
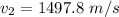
Hence, The projectile's speed as it passes the satellite is 1497.8 m/s.