Answer:
The quantity after t years 40
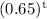 millions tons
millions tons
Explanation:
Given as :
The rate of decrease of carbon dioxide each other = 35%
The quantity of carbon dioxide emitted this year = 40 million tons
Let the quantity of carbon dioxide emitted after t year = A millions tons
Now, According to question
The quantity of carbon dioxide emitted after t year = The quantity of carbon dioxide emitted this year ×
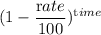
Or, A millions tons = 40 millions tons ×

Or, A millions tons = 40 millions tons ×
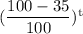
Or, A millions tons = 40 millions tons ×
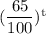
Or, A millions tons = 40 millions tons ×
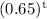
So,The quantity after t years = A = 40
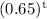 millions tons
millions tons
Hence The quantity after t years 40
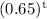 millions tons Answer
millions tons Answer