Question

At 297 K , to what pressure can the carbon dioxide in the cartridge inflate a 3.79 L mountain bike tire? (Note that the gauge pressure is the difference between the total pressure and atmospheric pressure. In this case, assume that atmospheric pressure is 14.7 psi.)

Answer 1

23.226 psi

Step-by-step explanation:

From the source,

The mass of the carbon dioxide is:- 16.0 g

Molar mass of carbon dioxide = 44.01 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

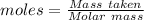
Thus,

`Moles= (16.0\ g)/(44.01\ g/mol)`

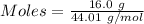
Moles of
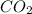`CO_2` = 0.3636 moles

Volume = 3.79 L

n = 0.3636 mol

Temperature = 297 K

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

P × 3.79 L = 0.3636 mol × 0.0821 L.atm/K.mol × 297 K

⇒P = 2.34 atm

Also, 1 atm = 14.7 psi

So, Pressure =
`2.34* 14.7` psi = 37.926 psi

THus, pressure by the gas is:-

P = Total pressure - Atmospheric pressure = 37.926 - 14.7 psi = 23.226 psi

The carbon dioxide in the cartridge inflate a 3.79 L mountain bike tire to 23.226 psi pressure.