Answer:
The line which is parallel to the given line
 is
is
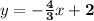
Explanation:
Given that the equation of the line is

To find the equation of the line is parallel to the given line equation.
We know that the given equation is in the slope intercept form
y=mx+c where m is the slope and c is the intercept.
Compare with given equation(1) we get
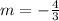 and c=1
and c=1
Now change the y intercept c=1 to a intercept of c= 2
Therefore (1) becomes
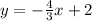
The above equation of the line is the parallel line to the given equation of the line