Answer:
y = 8 is the equation of tangent.
Explanation:
The equation of the tangent to the circle at (-6,8) is of the form:
y = mx + c
where m is the slope of the tangent and c is the y-intercept.
The point (-6,8) lies on the circle and the tangent line as well.
Hence (-6,8) satisfies the line equation:
8 = m(-6) + c ⇒ c-6m = 8 -------------1
We know that slope of two perpendicular lines are related as:
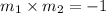
At any point on the circle, the normal line at a point is always perpendicular to the tangent line at that point.
Hence :
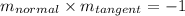
We can find the slope of the normal at point (-6,8) as it passes through the centre of the circle (-6,4) by using the two-points formula for slope.

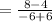
= ∞
Slope of the normal is infinity and hence slope of tangent is -1/∞ = 0
Hence m=0
Putting m=0 in equation 1 we get:
c = 8
The equation of tangent line at (-6,8) is:
y = 8