Answer:
2. a.
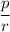
1.

Step-by-step explanation:
2. Extended Information on Trigonometric Ratios

__________________________________________________________
1. We have to determine which trigonometric ratio[s] to use, depending on what is given to us, and in this case, we will be using the secant [or cosine] ratio:
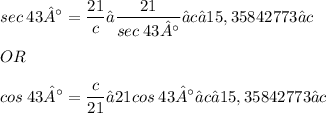
ONCE AGAIN...
Extended Information on Trigonometric Ratios

I am joyous to assist you anytime.