Question

Find the time required for an investment of $6000 to triple if the interest rate of 5.5% is compounded continuously.

Answer 1

Answer: t ≈ 20 years

Explanation:

Since it is compounded continuously , we will use the compound interest formula:

A = P
`e^(rt)`

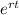
Where A is the amount when tripled

P is the initial amount

r is the rate

t is the time

since the investment is tripled , it means the A = 3P.

From the question:

A = 3P

P = $6000

r = 5.5%

t = ?

Substituting into the formula , we have

3P = P
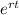`e^(rt)` , that is

3(6000) = 6000
`e^(0.055t)`

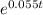
Dividing through by 6000 , we have

3 =
`e^(0.055t)`

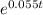
Take the In of both sides in order to remove the exponential , that is

In 3 = 0.055t

divide through by 0.055

t = In 3 / 0.055

Therefore :

t = 19.97476888

t≈ 20 years