Question

What would be the change in pressure in a sealed 10.0 L vessel due to the formation of N2 gas when the ammonium nitrite in 1.40 L of 1.40 M NH4NO2 decomposes at 25.0°C?

Answer 1

3.80 atm

Step-by-step explanation:

First of all, ammonium nitrite decomposes to produce nitrogen gas and liquid water at the given room temperature:

`NH_4NO_2 (s)\rightarrow N_2 (g) + 2 H_2O (l)`

Notice that the solid decomposes fully and produces the same number of moles of nitrogen:

`n_(NH_4NO_2) = n_(N_2)`

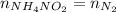
Find moles of ammonium nitrite multiplying its molarity by its volume:

`n_(NH_4NO_2) = c_(NH_4NO_2) V_(NH_4NO_2)`

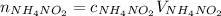
Express moles of nitrogen in terms of the ideal gas law:

`pV_(N_2)=n_(N_2)RT \therefore n_(N_2) = (pV_(N_2))/(RT)`

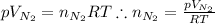
Substitute the two expressions above into the molar ratio equation:

`c_(NH_4NO_2) V_(NH_4NO_2)=(pV_(N_2))/(RT)`

Solve for the pressure:

`p = (c_(NH_4NO_2) V_(NH_4NO_2)RT)/(V_(N_2))=(1.40 M\cdot 1.40 L\cdot 0.08206 (L atm)/(mol K)\cdot 298.15 K)/(10.0 L)=4.80 atm`

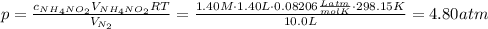
Notice that here R is the ideal gas law constant and we've converted the temperature into the absolute temperature:
`T = 25.0^oC + 273.15 K`.

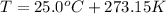Therefore, the overall final pressure would be 4.80 atm. Since initially we had air in the vessel at standard conditions (1.00 atm), the change in pressure would be 4.80 atm - 1.00 atm = 3.80 atm.