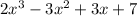Question

Find a polynomial function whose graph passes through(-1,-1)(0,7)(1,9)(2,17)

Answer 1

The required polynomial is f(x)=
`2x^(3)-3x^(2)+3x+7`

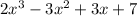
Explanation:

Given that polynomial is passing through points (-1,-1) (0,7) ( 1,9) and (2,17)

Let, The required polynomial be f(x)=
`ax^(3)+bx^(2)+cx+d`

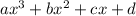
For point (-1,-1)

f(x)=
`ax^(3)+bx^(2)+cx+d`

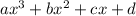
f(-1)=
`a(-1)^(3)+b(-1)^(2)+c(-1)+d`

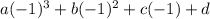
(-1)a+b-c+d=(-1) Equation 1

For point (0,7)

f(x)=
`ax^(3)+bx^(2)+cx+d`

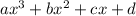
f(0)=
`a(0)^(3)+b(0)^(2)+c(0)+d`

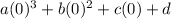
d=7 Equation 2

For point ( 1,9)

f(x)=
`ax^(3)+bx^(2)+cx+d`

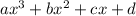
f(1)=
`a(1)^(3)+b(1)^(2)+c(1)+d`

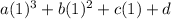
a+b+c+d=9 Equation 3

For point (2,17)

f(x)=
`ax^(3)+bx^(2)+cx+d`

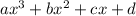
f(2)=
`a(2)^(3)+b(2)^(2)+c(2)+d`

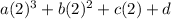
8a+4b+2c+d=17 Equation 4

Replacing value of d of equation 2 in equation 1,3,4

For equation 1:

(-1)a+b-c+d=(-1)

(-1)a+b-c=(-8)

For equation 3:

a+b+c+d=9

a+b+c=2

For equation 4:

8a+4b+2c+d=17

8a+4b+2c=10

Now,

On adding equation 1 and 3

For equation 1: (-1)a+b-c=(-8)

For equation 3: a+b+c=2

((-1)a+b-c)+(a+b+c)=(-8)+2

2b=(-6)

b=(-3)

Replacing value of b in equation 1 and 4:

For equation 1: (-1)a+b-c=(-8)

(-1)a+(-3)-c=(-8)

(-1)a-c=(-5) Equation 4

For equation 4: 8a+4b+2c=10

8a+4b+2c=10

8a+4(-3)+2c=10

8a+2c=22 Equation 5

For value of a and c:

Equation 4 can be write as

(-1)a-c=(-5)

a+c=5

a=5-c

Replacing value of a in equation 5

8a+2c=22

8(5-c)+2c=22

40-8c+2c=22

-6c=-18

c=3

So,

a=5-c=5-3=2

a=2

Thus,

The value of

a=2, b=(-3), c=3 and d=7

The required polynomial is

f(x)=
`ax^(3)+bx^(2)+cx+d`

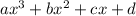
f(x)=
`2x^(3)-3x^(2)+3x+7`