Answer:
Each side of the original triangle is 2 times the length of each side of the scale drawing
Explanation:
Let
z ----> the scale factor
x ----> the measure of the side of the scale drawing
y --- measure of the side of the original triangle
we know that
The scale factor is equal to divide the measure of the scale drawing by the measure of the original triangle
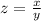
we have
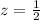
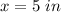
substitute
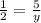
solve for y
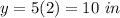
so
The measure of each side of the original triangle is 10 inches
therefore
Each side of the original triangle is 2 times the length of each side of the scale drawing