Answer:
8.00%
Step-by-step explanation:
Data provided in the question:
Selling price of the bond i.e current value = $270
Future value = $1,850
Maturity time, t = 25 years
Now,
Effective yield to maturity, r =
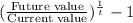
on substituting the respective values, we get
Effective yield to maturity, r =
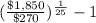
or
Effective yield to maturity, r = 1.0800 - 1
or
Effective yield to maturity = 0.0800
or
= 0.0800 × 100% = 8.00%