Question

A person is in a closed room (a racquetball court) with ????=453m3 hitting a ball (m=42.0g) around at random without any pauses. The average kinetic energy of the ball is 2.30 J. (a) What is the average value of ????2x? Does it matter which direction you take to be x? (b) Applying the methods of this chapter, find the average pressure on the walls? (c) Aside from the presence of only one "molecule" in this problem, what is the main assumption in Pressure, Temperature, and RMS Speed that does not apply here?

Answer 1

The average value of u² is 54.8 m²/s². It does not matter which direction is taken as x. The average pressure on the walls can be found using the force and area equations.

Step-by-step explanation:

(a) The average value of u² can be found by dividing the average kinetic energy by the mass of the ball: u² = KE / m. In this case, u² = 2.30 J / 0.042 kg = 54.8 m²/s².

It does not matter which direction you take to be x. The average value of u² will be the same regardless of the direction.

(b) The average pressure on the walls can be found using the equation P = F / A, where P is the pressure, F is the force, and A is the area of the walls. The force exerted on the walls can be found using the equation F = ∆p / ∆t, where ∆p is the change in momentum and ∆t is the change in time. Since there are no pauses in the ball's motion, ∆p = m * ∆v, where m is the mass of the ball and ∆v is the change in velocity. The average pressure will be the force divided by the area of the walls.

(c) The main assumption in Pressure, Temperature, and RMS Speed that does not apply here is that there are a large number of gas molecules moving in random directions. In this problem, there is only one molecule, so the assumption of a large number of molecules does not hold.

Answer 2

(a)
`v^(2) _(x) = 36.508 m^2/s^2`

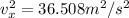
(b) 0.1235 Pa

(c) The volume of the ball is significant when compared with the volume of the closed room. Thus, the constant 'b' of the equation of Van der Waal is greater than zero.

Step-by-step explanation:

In the question, we are given the following variables:

V = 453 m^3

`m_(ball) = m = 42.0 g`

Kinetic energy (K.E) = 2.30 J

(a) The equation for kinetic energy is:

`K.E = (1)/(2)mv^(2)`

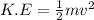
Since the average velocity components of the ball in the three dimensions are equal. Thus, we have:

`v_(x) ^(2) = v^(2) _(y) =v^(2) _(z)`

In addition:

`v^(2) =`
`v_(x) ^(2) + v^(2) _(y) +v^(2) _(z)` =
`3v^(2) _(x)`

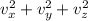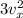
Therefore:

`K.E = (1)/(2)m[3v^(2) _(x)]` =
`(3)/(2)mv^(2) _(x)`

Thus:

`v^(2) _(x) = (KE)/(1.5*m) = (2.3)/(1.5*0.042) = 36.508 m^2/s^2`

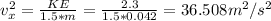
It does not matter which direction we take as x-direction because the average velocity component in every direction is the same.

(b) The average pressure on the walls can be calculated using the equation below:

`P =(mv^(2) _(x) )/(V)`

where V = 453 m^3

Thus: P = (0.042*36.508^2)/453 = 0.1235 Pa

(c) The volume of the ball is significant when compared with the volume of the closed room. Thus, the constant 'b' of the equation of van der Waal is greater than zero.