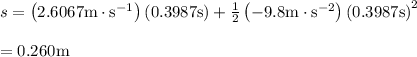Answer:
Step-by-step explanation:
Here is the full question and answer,
The archerfish is a type of fish well known for its ability to catch resting insects by spitting a jet of water at them. This spitting ability is enabled by the presence of a groove in the roof of the mouth of the archerfish. The groove forms a long, narrow tube when the fish places its tongue against it and propels drops of water along the tube by compressing its gill covers.
When an archerfish is hunting, its body shape allows it to swim very close to the water surface and look upward without creating a disturbance. The fish can then bring the tip of its mouth close to the surface and shoot the drops of water at the insects resting on overhead vegetation or floating on the water surface.
Part A: At what speed v should an archerfish spit the water to shoot down a floating insect located at a distance 0.800 m from the fish? Assume that the fish is located very close to the surface of the pond and spits the water at an angle 60 degrees above the water surface.
Part B: Now assume that the insect, instead of floating on the surface, is resting on a leaf above the water surface at a horizontal distance 0.600 m away from the fish. The archerfish successfully shoots down the resting insect by spitting water drops at the same angle 60 degrees above the surface and with the same initial speed v as before. At what height h above the surface was the insect?
Answer
A.) The path of a projectile is horizontal and symmetrical ground. The time is taken to reach maximum height, the total time that the particle is in flight will be double that amount.
Calculate the speed of the archer fish.
The time of the flight of spitted water is,
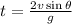
Substitute
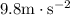 for g and
for g and
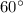 for
for
 in above equation.
in above equation.
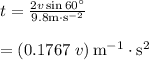
Spitted water will travel
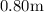 horizontally.
horizontally.
Displacement of water in this time period is
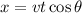
Substitute
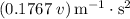 for
for
![t\rm 60^\circ[tex] for [tex]\theta](https://img.qammunity.org/2020/formulas/physics/college/5b66eftkppxr06oa4q4y3d0im3e0xpsbyt.png) and
and
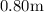 for x in above equation.
for x in above equation.

B.) There are two component of velocity vertical and horizontal. Calculate vertical velocity and horizontal velocity when the angle is given than calculate the time of flight when the horizontal distance is given. Value of the horizontal distance, angle and velocity are given. Use the kinematic equation to solve the height of insect above the surface.
Calculate the height of insect above the surface.
Vertical component of the velocity is,
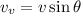
Substitute
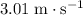 for v and
for v and
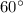 for
for
 in above equation.
in above equation.
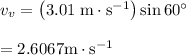
Horizontal component of the velocity is,
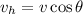
Substitute
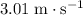 for v and
for v and
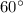 for
for
 in above equation.
in above equation.
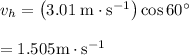
When horizontal
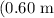 distance away from the fish.
distance away from the fish.
The time of flight for distance (d) is ,
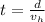
Substitute
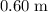 for d and
for d and
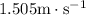 for
for
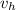 in equation
in equation
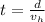
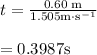
Distance of the insect above the surface is,
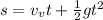
Substitute
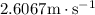 for
for
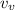 and
and
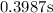 for t and
for t and
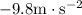 for g in above equation.
for g in above equation.