Answer:
The number of each coin she have are 17 dimes and 14 nickels.
Explanation:
Given:
A coin collector has 31 dimes and nickels with a total face value of $2.40.
Now, to find each does she have.
Let the number of dimes be
 .
.
Let the number of nickels be
 .
.
So, total number of coins are:
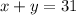
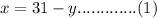
Value of a dime = 10 cents
Value of a nickel = 5 cents
Total face value = 240 cents
(1$ = 100 cents. $2.40×100 =240 cents)
Now, total value of coins:
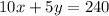
Putting the equation (1) in the place of
 :
:
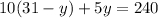
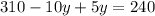
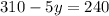
Moving variables on one side and the numbers on other:
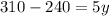
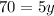
Dividing both sides by 5 we get:

The number of nickels = 14.
Now, putting the value of
 in equation (1) we get:
in equation (1) we get:
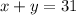
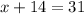
Subtracting both sides by 14 we get:

The number of dimes = 17.
Therefore, the number of each coin she have are 17 dimes and 14 nickels.