Answer:
a.
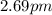
b.
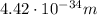
Step-by-step explanation:
The de Broglie wavelength can be found by the following equation:
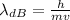
Here:
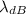 is the de Broglie wavelength (in m);
is the de Broglie wavelength (in m);
 is the Planck's constant,
is the Planck's constant,
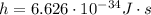 ;
;
 is mass (in kg);
is mass (in kg);
![v[tex] is velocity (in m/s).</p><p>a. We need to know the mass of an electron here:</p><p>[tex]m_e=9.11\cdot10^(-31) kg](https://img.qammunity.org/2020/formulas/chemistry/middle-school/rc488bqphgs48ixolxhgnigg6utksiru7r.png)
And the speed of light:
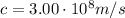
The fraction of the speed of light is:
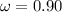
Substituting into the equation:
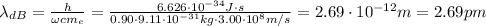
b. Similarly, here we have:
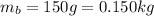
And the velocity of:
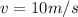
We obtain:
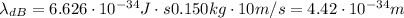
Notice that the wavelength of a large object is smaller by a fraction of:
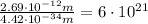
This means the de Broglie wavelength of a macroscopic object is negligible compared to the wavelength of a microscopic object.