Answer:
The required probability is given by, 0.9919.
Explanation:
Let, X be the random variable denoting the no. of pages among those 4 pages which Julia writes where she makes no spelling mistake.
clearly,
X
 Binomial (4, 0.7)
Binomial (4, 0.7)
So, P(X = x) =
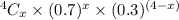
[when x = 0, 1, 2, 3, 4]
= 0 otherwise
According to the question, we are to find out P(X ≥ 1) .
Now, P(X ≥ 1)
= 1 - P(X = 0)
=
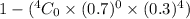
=
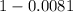
= 0.9919
So, the required probability is given by, 0.9919