Question

Gastric juice is made up of substances secreted from parietal cells, chief cells, and mucous-secreting cells. The cells secrete HCl, proteolytic enzyme zymogens, mucin, and intrinsic factor. The pH of gastric juice is acidic, between 1-3. If the pH of gastric juice is 2.1, what is the amount of energy (?G) required for the transport of hydrogen ions from a cell (internal pH of 7.4) into the stomach lumen? Assume that the potential difference across the membrane separating the cell and the interior of the stomach is �60.0 mV (inside of cells negative relative to the lumen of the stomach).

Assume that the temperature is 37 �C.

The Faraday constant is 96.5 kJ�V�1�mol�1 and the gas constant is 8.314� 10�3 kJ�mol�1�K�1. Express your answer in kJ/mol.

Answer 1

The amount of energy required to transport hydrogen ions from a cell into the stomach is 37.26KJ/mol.

Explanation:

The free change for the process can be written in terms of its equilibrium constant as:

ΔG° =
`-RTInK_(eq)`

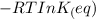
where:

R= universal gas constant

T= temperature

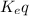`K_eq`= equilibrum constant for the process

Similarly, free energy change and cell potentia; are related to each other as follows;

ΔG= -nFE°

from above;

F = faraday's constant

n = number of electrons exchanged in the process; and

E = standard cell potential

∴ The amount of energy required for transport of hydrogen ions from a cell into stomach lumen can be calculated as:

ΔG° =
`-RTInK_(eq)`

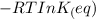
where;

[texK_eq[/tex]=
`([H^+]_(cell))/([H^+(stomach lumen)])`

For transport of ions to an internal pH of 7.4, the transport taking place can be given as:

`H^+_(inside)` ⇒
`H^+_(outside)`

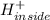Equilibrum constant for the transport is given as:

`K_(eq)=([H^+]_(outside))/([H^+]_(inside))`

`=([H^+]_(cell))/([H^+]_(stomach lumen))`

`[H^+]_(cell)`= 10⁻⁷⁴

=3.98 * 10⁻⁸M

`[H^+]_(stomach lumen)` = 10⁻²¹

=7.94 * 10⁻³M

Hence;

`K_(eq)=([H^+]_(cell))/([H^+]_(stomachlumen))`

=
`\frac{3.98*10^(-8)}{7.94*10{-3}}`

= 5.012 × 10⁻⁶

Furthermore, free energy change for this reaction is related to the equilibrium concentration given as:

ΔG° =
`-RTInK_(eq)`

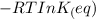
If temperature T= 37° C ; in kelvin

=37° C + 273.15K

=310.15K; and

R-= 8.314 j/mol/k

substituting the values into the equation we have;

ΔG₁ =
`-(8.314J/mol/K)(310.15)TIn(5.0126*10^(-6))`

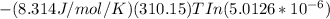
= 31467.93Jmol⁻¹

≅ 31.47KJmol⁻¹

If the potential difference across the cell membrane= 60.0mV.

Energy required to cross the cell membrane will be:

ΔG₂ =
`-nFE°_(membrane)`

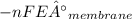
ΔG₂ =
`-(1 mol)(96.5KJ/mol/V)(60*10^(-3))`

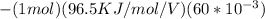
= 5.79KJ

Therefore, for one mole of electron transfer across the membrane; the energy required is 5.79KJmol⁻¹

Now, we can calculate the total amount of energyy required to transport H⁺ ions across the membrane:

Δ
`G_(total) = G_(1)+G_(2)`

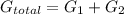
= (31.47+5.79) KJmol⁻¹

= 37.26KJmol⁻¹

We can therefore conclude that;

The amount of energy required to transport ions from cell to stomach lumen is 37.26KJmol⁻¹