Answer:
Y component = 32.37
Step-by-step explanation:
Given:
Angle of projection of the rocket is,
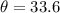
Initial velocity of the rocket is,
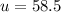
A vector at an angle
 with the horizontal can be resolved into mutually perpendicular components; one along the horizontal direction and the other along the vertical direction.
with the horizontal can be resolved into mutually perpendicular components; one along the horizontal direction and the other along the vertical direction.
If a vector 'A' makes angle
 with the horizontal, then the horizontal and vertical components are given as:
with the horizontal, then the horizontal and vertical components are given as:
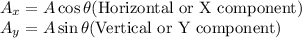
Here, as the velocity is a vector quantity and makes an angle of 33.6 with the horizontal, its Y component is given as:
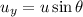
Plug in the given values and solve for
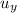 . This gives,
. This gives,
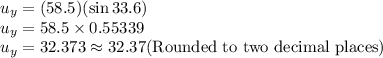
Therefore, the Y component of initial velocity is 32.37.