Question

For each of the following vector fields F, decide whether it is conservative or not by computing curl F. Type in a potential function f (that is, ∇f=F). Assume the potential function has a value of zero at the origin. If the vector field is not conservative, type N.1. F(x,y)=(-6x+5y)i+(5x+10y)j

2. F(x,y,z)=-3xi-2yj+k
3. F(x,y)=(-siny)i+(10y-3xcosy)j
4. F(x,y,z)=-3x^2i+5y^2j+5z^2k

Answer 1

1,2 and 4 are conservatives

3 is not conservative

Explanation:

We calculate the Curl F

Remember that:

Curl F = <
`(dFz)/(dy) - (dFy)/(dz), (dFz)/(dx) - (dFx)/(dz), (dFy)/(dx) - (dFx)/(dy)`>

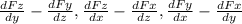1. Curl F = <0,0,5-5> = <0,0,0>

The potential function f so that ∇f=F

f(x,y,z) =
`-3x^(2) +5xy + 5y^(2)`

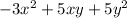
Then F is conservative

2. Curl F = < 0, 0 ,0>

The potential function f so that ∇f=F

f(x,y,z) =
`-3/2x^(2) -y^(2)+z`

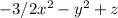
Then F is conservative

3. Curl F = <0 ,0, 10+3xsin(y) - (-cos(y))>

= <0 ,0 , 10 +3xsin(y) + cos(y)<

How the field's divergence is not zero the vector field is not conservative

4. Curl F = <0, 0, 0>

The potential function f so that ∇f=F

f(x,y,z) =
`x^(3)+(5/3)y^(3)+(5/3)z^(3)`

Then F is conservative